Astrometry

Field distortion

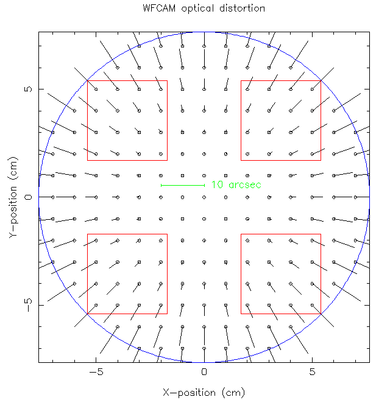
The figure on the left demonstrates the level of the optical distortion over the field of view of WFCAM. The non-linear term introduces a (pincushion/barrel) distortion amounting to roughly 10 arcsec from the centre to the edge of the 0.8 degree diameter field, denoted by the blue circle.

Most of this distortion can be accounted for by a cubic radial term. This is included in the WCS solution as the PV2_3 term. Early results indicated that this was -50 for all passbands. A more detailed analysis has shown that this term is different for each passband and simply tuning to the passband has reduced the maximum systematic residual by a factor of 2 from a maximum of ~100mas to ~50mas for the absolute astrometry using the WCS from the FITS headers.

The PV2_3 values for each passband are

Z = -44.0, Y = -45.0, J = -46.0, H = -50.0 and K = -60.0.

The next step is to further adjust the cubic term and to try a fifth-order term since there is clear evidence of a higher-order radial term at the level of 50mas in the outer parts of the field of view.

Note that 06B data and later uses a different value for each passband. Data earlier than this uses PV2_3=-50 for all passbands.

Differential distortion

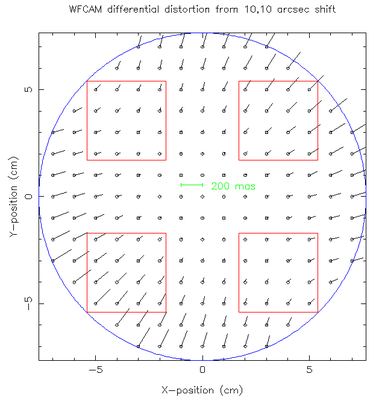
An example of the differential non-linear distortion on sky arising from a shift along a diagonal of 10,10 arcsec is shown on the figure on the left. This would be the extreme ends of, say, dithering within a +/-5 arcsec box-like region centred on a target pointing. As a reference the pixel scale for WFCAM is 0.40 arcsec/pixel.

We can quantify this effect in a more useful manner by forming

dr_true/dr' = 1 + 3k x r'^2

which describes the local change in relative pixel scale as a function of radial distance. For example, for WFCAM at around 0.45 deg radius, the second term is about 1.0% in size (ie. 3x the radial distortion value shown in the earlier plots). This means that a 10 arcsec shift in the centre corrsponds to a 10.1 arcsec shift at the outer corners of the arrays. The majority (~90%) of this distortion occurs across individual detectors. Therefore, even after re-registering the detector centre, there would still be a distortion at the +/-0.05 arcsec level across it.

The pipeline processing essentially corrects for the radial distortion and then solves for the following linear transformation from (distorted) standard coordinates with respect to the optical axis

xi' = a * x + b * y + c xn' = d * x + e * y + f

where a, e, b, d encode for scale(s), rotation and shear, and c and f are offsets.

Effect of scale change on photometry

In addition to astrometric effects the change in scale as a function of radius also creates photometric complications. The aim of conventional flatfielding is to create a flat background by normalising out perceived variations from uniformly illuminated frames. If the sky area per pixel changes then this is reflected in a systematic error in the derived photometry. However, since it is much simpler to deal with "flat" backgrounds, this problem is either usually ignored or corrected during later processing stages, together with other systematic photometry effects. The effect is simplest to envisage by considering what happens to the area of an annulus on sky when projected onto the detector focal plane. The sky annulus of 2.pi.s.ds becomes 2.pi.r'.dr' on the detector, which using k to denote k3/k1 leads to an relative area of

(1 + k x r'^2).(1 + 3k x r'^2) =~ (1 + 4 x k x r'^2)

or in other words roughly 4x the linear scale distortion.

At the corners of the field WFCAM has a worst case (K-band) linear scale distortion of about 0.3% leading to photometry systematics due to this effect of at most ~1.2% relative to the centre, and can probably be safely ignored for most applications.

To illustrate the effect the colourful image on the left shows the systematics in photometry that would arise from a standard WFCAM 4 pointing tile. The systematics vary from 0% in the centre up to 0.5% lighter shades of green, through purple and red at 1.0% to yellow, 1.5% in the corners. The field of view shown is roughly 0.8 deg x 0.8 deg.

Atmospheric Differential Refraction in the Infrared

The effect of atmospheric differential refraction in the infrared as a function of colour is small. The only measurable effect is seen in the J passband and the magnitude of the effect is of order 1 mas. In comparison, the astrometric accuracy for WFCAM at the bright end is expected to be around 20 mas.

World Coordinate System and FITS headers

The standard way of defining a World Coordinate System (WCS) for telescopes with focal stations requiring a general radial distortion model, is to use a Zenithal PolyNomial (ZPN) projection. For details of this consult: Calabretta & Greisen 2002 A&A 395 1077 and Greisen & Calabretta 2002 A&A 395 1061.

An example WCS extracted from an actual WFCAM header for detector #1 is given below:

CTYPE1  = 'RA---ZPN'           / Algorithm type for axis 1
CTYPE2  = 'DEC--ZPN'           / Algorithm type for axis 2
CRPIX1  =        2.9950000E+03 / [pixel] Reference pixel along axis 1
CRPIX2  =       -9.7296002E+02 / [pixel] Reference pixel along axis 2
CRVAL1  =        1.5847932E+02 / [deg] Right ascension at the reference pixel
CRVAL2  =        5.5045403E+01 / [deg] Declination at the reference pixel
CRUNIT1 = 'deg     '           / Unit of right ascension co-ordinates
CRUNIT2 = 'deg     '           / Unit of declination co-ordinates
CD1_1   =       -8.6063899E-08 / Transformation matrix element
CD1_2   =       -1.1131840E-04 / Transformation matrix element
CD2_1   =        1.1132305E-04 / Transformation matrix element
CD2_2   =       -1.8366745E-07 / Transformation matrix element
PV2_1   =             1.00E+00 / Pol.coeff. for pixel -> celestial coord
PV2_2   =         0.000000E+00 / Pol.coeff. for pixel -> celestial coord
PV2_3   =            -5.00E+01 / Pol.coeff. for pixel -> celestial coord