Photometric Calibration
The photometric calibration of WFCAM is described in Hodgkin et al. 2009:
abstract: http://cdsads.u-strasbg.fr/doi/10.1111/j.1365-2966.2008.14387.x
astroph: http://fr.arxiv.org/abs/0812.3081
MNRAS pdf: http://www3.interscience.wiley.com/cgi-bin/fulltext?ID=122210794&PLACEBO=IE.pdf&mode=pdf
A brief summary follows.
All WFCAM data are processed in Cambridge with a pipeline developed by CASU and documented in Irwin et al. (2008). On this page we describe the steps used to measure magnitudes and then apply a photometric calibration for each WFCAM image and subsequent catalogue. After processing and calibration, the WFCAM data (in the form of FITS binary images and catalogues) are transferred to Edinburgh for ingestion into the WFCAM Science Archive (WSA, Hambly et al. 2008). The UKIDSS data have now seen a number of data releases from the WSA, and the photometric calibration has evolved to tackle the (increasingly smaller) corrections needed to meet the survey goals; the corrections included in each release are summarised in the table.
Summary of photometric calibration corrections included in each UKIDSS release from the WSA. The columns indicate which of the following are accounted for: a reddening dependent correction, a per-chip zeropoint, a radial distortion term, and a residual 2D spatial systematic correction.
| Release | Date | E(B-V)' | chip ZP | radial | spatial |
|---|---|---|---|---|---|
| EDR | Feb 06 | no | no | no | no |
| DR1 | Jul 06 | no | no | no | no |
| DR2 | Mar 07 | yes | no | no | no |
| DR3 | Dec 07 | yes | yes | no | no |
| DR4 | Jul 08 | yes | yes | yes | yes |
Measurement of instrumental magnitudes
The source extraction software (Irwin et al. 2008) measures an array of background-subtracted aperture fluxes for each detected source, using 13 soft-edged circular apertures of radius r/2, r/sqrt(2), r, sqrt(2)r, 2r ... up to 12r, where r=1 arcsecond. A soft-edged aperture divides the flux in pixels lying across the aperture boundary in proportion to the pixel area enclosed. In this paper we only consider photometry derived from fluxes measured within an aperture of radius 1 arcsecond. However, all the apertures of selected isolated bright stars are used to determine the curve-of-growth of the aperture fluxes, i.e. the enclosed counts as a function of radius. This curve of growth is used to measure the point spread function (PSF) aperture correction for point sources for each detector, for each aperture (up to and including 4r, which includes typically about 99 per cent, or more, of the total stellar flux). Irwin et al. (2008) find that this method derives aperture corrections which contribute <= 1 per cent to the overall photometry error budget.
Radial Distortion
A further correction should be applied to the source flux to account for the non-negligible field distortion in WFCAM, described in detail in Irwin et al. (2008). The astrometric distortion is radial and leads to an increase in pixel area by around 1.2 per cent compared to the centre of the field of view. Standard image processing techniques assume a uniform pixel scale, and that a correctly reduced image will have a flat background. For WFCAM's variable pixel scale, this is actually incorrect and one would expect to see an increase in the sky counts per pixel at large off-axis angles, while the total number of counts detected from a star would be independent of its position on the array. The flatfielding of an image therefore introduces a systematic error into the photometry of sources towards the edge of the field of view. The corrected flux f_cor, where f is defined as the aperture corrected count-rate in ADU per second of the source above background, is simply:
f_{\rm cor} = f / ( 1 + 3 k_3 r^2 ) ( 1 + k_3 r^2 )
Where k_3 (with units of radian/radian$^3$) is the coefficient of the third order polynomial term in the radial distortion equation (Irwin et al. 2008) and is found to be slowly wavelength dependent with a value of -50.0 in the H-band (called PV2_3 in the FITS headers). The instrumental magnitude is then
m_i=-2.5log_{10}(f_{\rm cor})
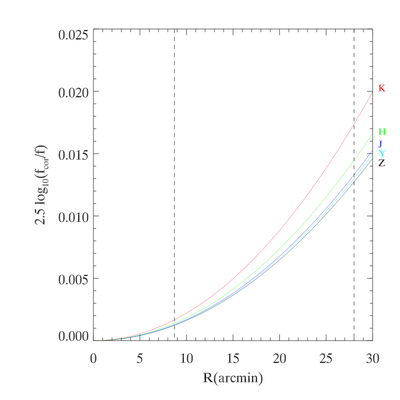
This correction has not been applied for WSA releases DR1--DR3 (Hambly et al. 2008), but is included for DR4 and subsequent releases. The figure below plots the radial distortion term (f_{\rm cor}/f converted to magnitudes) as a function of off-axis angle for the WFCAM filters.
The WFCAM Photometric System
Photometry is currently based on 2MASS, via colour equations to convert to the WFCAM instrumental system. 2MASS solutions for every catalogued frame are generated and allow monitoring of effective ZPs at the ~few % level. A series of tests using the UKIRT FS observations to monitor the WFCAM 2MASS calibration are being carried out, with very promising results (see the reports at the bottom of this page for more detail). This analysis suggests that the 2MASS calibration is indeed delivering product frame-by-frame photometric zero-points (with factored-in extinction tracking) at the +/-2% level and looks highly likely to meet the WFCAM photometric calibration requirements. This is mainly due to the huge effort the 2MASS survey team made in ensuring a reliable all-sky calibration.
The latest calibrations (December 2006) show that the colour equations are as follows:
Z_wfcam = J + 0.95*(J - H)
Y_wfcam = J + 0.50*(J - H) + 0.08
J_wfcam = J - 0.065*(J - H) used for DR2 and for 06B and later
H_wfcam = H + 0.070*(J - H) - 0.03
K_wfcam = K + 0.010*(J - K)
where the offsets in Y and H are to put WFCAM on the Vega system.
In deriving the photometric zero-point per field we also make a correction for Galactic extinction toward each star used proportional to E(B-V)' , the Bonifacio, Monai & Beers (2000) correction to the Schlegel et al. extinction map values i.e.
if E(B-V) > 0.1 then E(B-V) -> 0.1+0.65* [E(B-V) - 0.1]
where E(B-V) is computed using bilinear interpolation from the 4 nearest Schlegel map pixels.
The coefficients used are: 0.39, 0.16, 0.015, 0.005, 0.005 for Z, Y, J, H, K respectively in the sense of increasing the inferred zero-point.
With these new colour equations and a much better run of data we have rederived the system zero-points (corrected to unit airmass) for the main passbands. These are shown in the next table. Note also that in deriving these zero-points, all detectors have been gain-corrected to the average detector system
Z Y J H K Overall zero-point (count/s) 22.84 22.77 23.02 23.24 22.57 WFCAM (e-/s) 24.4 24.4 24.6 24.8 24.2 [using an average gain of 5.1 = 4.3 after correcting for intrapixel capacitance] UFTI (e-/s) ---- ---- 24.5 24.7 24.2
This gives the following WFCAM sensitivity figures for 5s exposures, 0.6 arcsec seeing and a 2 arcsec diameter aperture. Aperture corrections to/from other data should assume a Moffat profile with beta=2, which gives a 0.15 magnitude aperture loss in this case (included in the computation).
Z Y J H K
5-sigma limiting mag (5s) 19.6 19.0 18.4 17.8 17.1
(40s) 20.7 20.1 19.5 18.9 18.2
Sky (mag/sq arcsec) 18.0 17.0 15.6 14.0 13.4
Photometric Accuracy
zeropoint within 0.05 magnitudes of the median value for all observations made with the filter (incidentally, sigmaZP=0.03 magnitudes in all pass bands). We exclude sources at the very edges of the array, within 10 arcseconds of the detector edges.
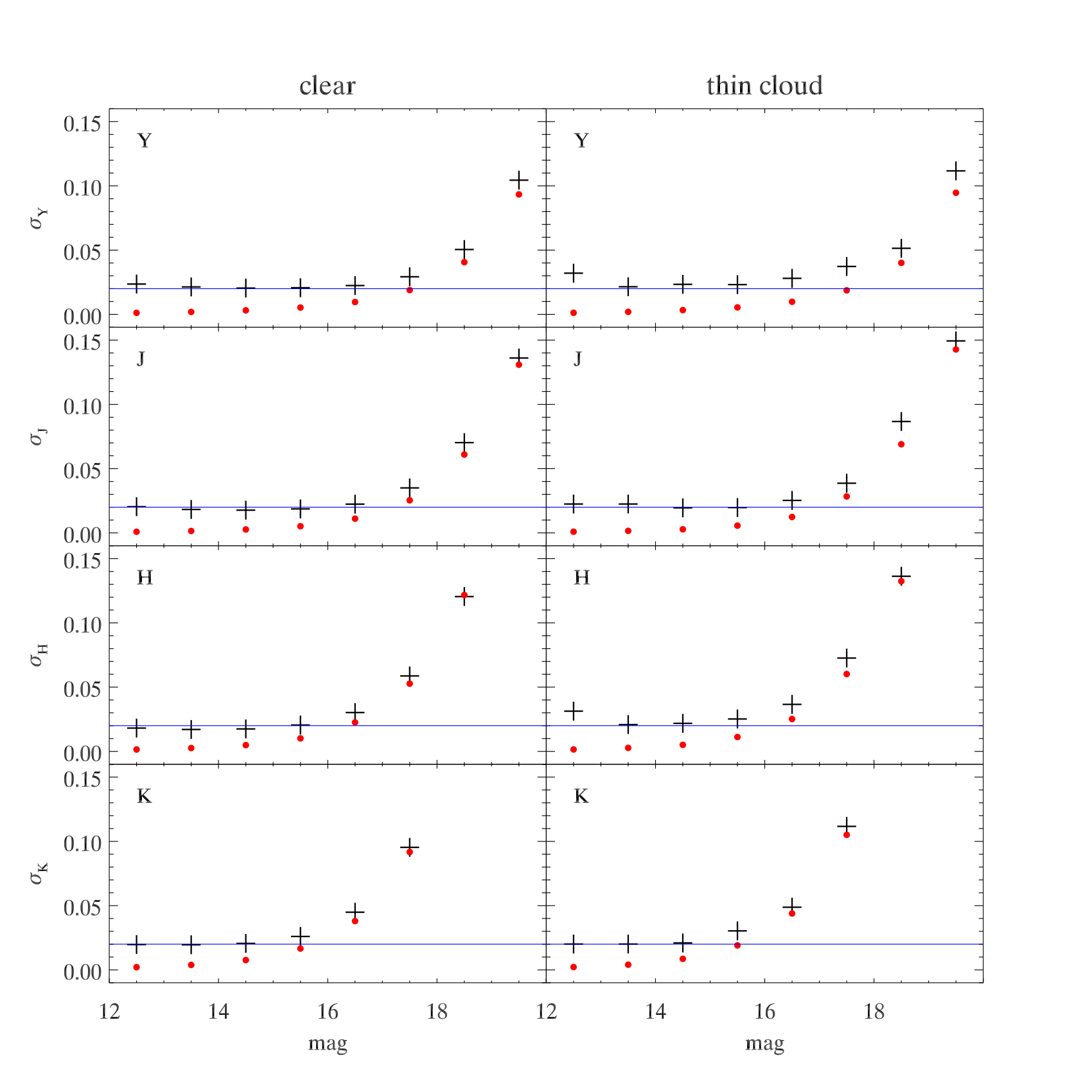
For a photometric calibration good to 2 per cent, then the median magnitude difference should be zero, and the standard deviation of the distribution for the brighter stars should be σ/sqrt(2) = 0.02. At the bright end, the Gaussian sigma (indicated by the black crosses in the Figure) is very close to the survey goal of 2 per cent. The pipeline errors (red dots) significantly underpredict the observed distribution, indicating that systematic errors are dominating at the 2 per cent level. The median systematic error across all magnitude bins, in all filters, required to bring the pipeline errors into agreement with the measured errors when added in quadrature is 0.020 magnitudes.
The zeropoint for each frame acts as a direct measure of the transmission of the atmosphere. The presence of clouds leads to a reduction in the derived zeropoint. In the above Figure we compare the rms distributions for stars taken in different conditions. conditions. Good conditions are defined above as having a frame zeropoint within 0.05 magnitudes of the median zeropoint for the filter. We compare this with the case of non-photometric conditions. where the frame zeropoint is more than 0.1, but no more than 0.2, magnitudes below the nominal survey zeropoints for each filter. This demonstrates that, even in non-photometric conditions, where more than 10 per cent of the stellar flux is lost to cloud, the calibration is still remarkably good, and only marginally (if at all) worse than the calibration derived in good conditions. The median systematic difference between the pipeline and measured errors is slightly larger at 0.026 magnitudes than measured in clear conditions, indicative of a small extra contribution from non-photometricity.

Y-BAND ZEROPOINT OFFSET
The Y-band calibration derived prior to DR3 showed a large offset with respect to a Vega system (see Figure). The blue star sequence clearly does not pass through (0,0), but is significantly shifted to the blue in Y-J. The figure shows that there is a non-linearity in the transformation between the J-K and Y-J colours for blue stars. Hence this offset is a natural consequence of a calibration based on the red stars, assuming a linear relation. ML fitting of the Y-band offset finds ΔY=-0.078 +/- 0.010. No offset is found for the ZJHK-bands (within measurement error).
SPATIAL SYSTEMATICS
Previous analysis of the WFCAM illumination correction variation for semesters O5A, 05B and 06A concluded that a factor of two improvement of the systematics in the photometry could be achieved by the simple expedient of using 2MASS residual-derived corrections to update the individual detector zero-points. With two more semesters (06B and 07A) now available we have re-examined these corrections using the procedure outlined below.
The object catalogues associated with each WFCAM science product frame are used in the pipeline calibration process to compute a single per pointing overall zero-point for the array of 4 detectors, using the colour equations specified above. The residuals from all 2MASS stars used in the frame zero-point determination (i.e. J, H, K signal:noise > 10:1) are also computed on a per pointing basis together with their standard coordinate location (Xi, Eta) with respect to the tangent point of the telescope optical axis. We use standard coordinates since these are independent of the degree of interleaving, and hence pixel scales, used in constructing the science product images and catalogues.
These datasets are then partitioned by month to correspond with the changover of the master flat field frames, with which we anticipate some of the corrections are correlated. Although we have labelled this as an illumination correction problem there are several other possible causes in addition to residual scattered light in the flat fields. These include: small differences in the colour equations between the detectors; low level non-linearity in the counts recorded by the detectors (direct efforts to quantify this measure no significant effect at the +/- 1 per cent level); and pedestal DC level offsets in the monthly master flat field frames (we see evidence for this at the per cent level in the derived sky corrections).
For each month of data and for each filter we then compute a per star zero-point relative to the previously computed overall zero-point for each science product image for the entire array. These differences are then stacked within a fixed standard coordinate grid, of cell size about 1.2 times 1.2 arcmin covering the complete array of 4 detectors, making use of selected data from each month of observations. Only science products taken in (almost) photometric conditions are used in this process to minimise the effects of non-photometric residual structure. The average offsets in the grid of values are then filtered (smoothed) using a combination of a two-dimensional 3 pixel bimedian and bilinear filter. This latter step ensures a smooth variation of values over the grid by effectively correlating the corrections on a scale of neighbouring grid points. This latter step is necessary since, even with a month of data, the number of points per cell is still only typically 25-100. The rms noise per cell from the 2MASS errors alone is still then at approximately the 1 per cent level. With smoothing this noise drops to the few milli-mag level which is a negligible extra error with respect to the derived corrections.
The residuals for each detector are then grouped and the median correction noted. These then define the detector-level zero-point corrections for each passband. The final stage is to apply the detector-level corrections and compute the residual systematics which are recorded as a correction table, and diagnostic plot. An example of the latter is shown here and the the possible origins of these patterns are discussed later.
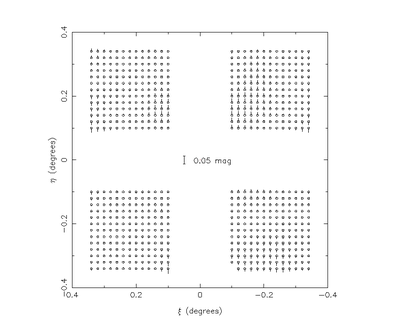
After removing the detector-level differences recurring generic patterns are visible in the final illumination correction, even across different passbands. This strongly suggests a common underlying cause and the three most likely factors are: low-level nonlinearity in the detectors - in which case the systematics should correlate with the flatfield properties; scattered light in the camera which would negate the implicit assumption of, on average, uniform illumination of the field; and spatially dependent PSF corrections - the residual maps are made from aperture-corrected 2 arcsec diameter flux measurements.
We have ruled out spatial PSF distortions being a significant contributor by comparing aperture-corrected 4 arcsec diameter fluxes with the 2 arcsec diameter measures. If we exclude 05A observations, when adjustments to the focal plane geometry were still being made, the average systematic difference between 2 and 4 arcsec diameter stellar fluxes is negligible (<1 per cent) over the entire array. It is more difficult to eliminate subtle scattered light problems as the underlying cause but we note that similar spatial patterns generally occur in all filters in all the semesters. This together with the detailed analysis of the extremely low level (<10-5) of expected scattered light undertaken during camera design and construction, suggest that this is also unlikely to be the primary cause of these systematics. It is relatively straightforward to test for the effects of non-linearity by directly comparing residual photometry systematics with the differential variation in the flatfield level over each detector. It appears that the detectors with the largest and smallest flatfield variations (#1 and #4) show no effects at the 1 per cent level; whereas detectors #2 and #3 show a clear correlation between residual magnitude spatial systematics and flatfield level. This work is currently ongoing.
Photometric recalibration of all processed data (05A,05B,06A,06B,07A) has been completed in time for UKIDSS DR3. This includes correcting the Y-band zero-point and providing individual detector zero-point corrections (typically 1-2 per cent) based on the monthly analysis described here. The remaining photometry residual systematics as a function of spatial location in the array are available as monthly tables and figures, detailing the remaining correction to be optionally applied. These remaining effects are generally low level, around 1 per cent, but in certain regions and/or passbands can be several times larger.

